Heron's Formula

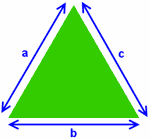
 triangle sss

Area of a Triangle from Sides

You can calculate the area of a triangle if you know the lengths of all three sides, using a formula that has been known for nearly 2000 years.

It is called "Heron's Formula" after Hero of Alexandria (see below)

 

Just use this two step process:

Step 1: Calculate "s" (half of the triangles perimeter):

s = a+b+c2

Step 2: Then calculate the Area:

herons formula A = sqrt( s(s-a)(s-b)(s-c) )

Example: What is the area of a triangle where every side is 5 long?

Step 1: s = 5+5+52 = 7.5
Step 2: A = √(7.5 × 2.5 × 2.5 × 2.5) = √(117.1875) = 10.825...Try it yourself:

Heron's Formula
Find a Triangle's Area from its Sides
Classic Heron's Formula:
s = (a+b+c)/2 = 6
Area = √( s(s-a)(s-b)(s-c) )
Area = 6
Variation with less rounding error:
Sides in Descending Order: 5,4,3
Area = √((a+(b+c))(c-(a-b))(c+(a-b))(a+(b-c)))/4
Area = 6
a:53.1301°
b:36.8699°
c:90°
Area is
6.000000
© 2018 MathsIsFun.com v0.61

 

xAS

Hero of Alexandria

The formula is credited to Hero (or Heron) of Alexandria, who was a Greek Engineer and Mathematician in 10 – 70 AD.

Amongst other things, he developed the Aeolipile, the first known steam engine, but it was treated as a toy!

Angles

In the calculator above I also used the Law of Cosines to calculate the angles (for a complete solution). The formula is:

triangle angle from sides C = cos^-1( (a^2+b^2-c^2)/2ab )

Where "C" is the angle opposite side "c".

Comments

Post a Comment

If you have any doubts let me know

Popular posts from this blog

INTRODUCTION TO SURFACE AREA AND VOLUME

Image
  Surface Area Surface area refers to the area of the exposed surface of the three dimensional solid. There are two types of surface area (i) Lateral surface area  (ii) Total surface area In general, lateral surface area does not include the base of the shape.  Total surface area is the area of the entire object. Lateral surface area (lateral also means side), does not include the area of the top and bottom. Volume The volume of any solid refers to the three dimensional space it occupies, often quantified numerically.One dimensional figures, namely lines and two dimensional shapes, namely squares area assigned zero volume in the  three dimensional space. Formulas Cube : A cube is a right rectangular prism with square upper and lower bases and a square vertical faces. Cuboid : A  cuboid  is a three-dimensional shape with a length, width, and a height. The  cuboid  shape has six sides called faces Cone : A cone is a solid with circular base curved by a curved surface to a single vertex .
Read more

Coordinate Geometry

Image
  Maths   >   Coordinate Geometry   >   Coordinate Geometry Coordinate Geometry Do you remember what a plane is? A plane is any flat  surface  which can go on infinitely in both of the directions. Now, if there is a  point on a plane , you can easily locate that point with the help of coordinate geometry. Using the two numbers of the coordinate geometry, a location of any point on the plane can be found. Let us know more! A coordinate geometry is a branch of geometry where the position of the points on the plane is defined with the help of an ordered pair of numbers also known as  coordinates . What are Coordinates? Now, to help you understand the coordinates, take a look at the figure below. Now, consider the grid on the right. The columns of the grid are labeled as A, B, C, D, E, F, etc. On the other hand, the rows are numbered as 1, 2, 3, 4, 5, 6, and so on. You can see that the letter X is located in the box D3 i.e. column D and row 3.  Here, D and 3 are the coordinates of th
Read more